The number of figures in a result that are reliable enough to be known is known as the number of important figures. It is stated that there are three major figures in 13.2. It is claimed that 13.20 has four significant figures. The significant or key digits in a given number are those that, based on precision, accurately express the meaning of the number. For instance, there are four significant numbers in 6.658. These huge numbers give the accuracy of the numbers. They go by the name of significant digits as well.
Contents
Rounding Important Numbers
One or more digits are left from the right to round a number to the required number of significant digits. The last digit kept should not change if the first digit on the left is less than 5. The last digit is rounded up if the first digit is larger than 5. The retained integer is rounded up or down to an even number when the digit remaining is precisely 5. Rounding off should be done as a whole rather than one digit at a time when multiple digits are remaining. We will discuss the Sig Fig Calculator here.
To round off the significant numbers, there are two rules:
First, we need to determine the digit up to which the rounding off should be done. We must eliminate every integer on the right side of the total after the rounding off digit is less than 5.
However, we must add 1 to the rounding-off digit and eliminate the other numbers on the right side if the digit adjacent to the rounding-off digit is higher than 5.
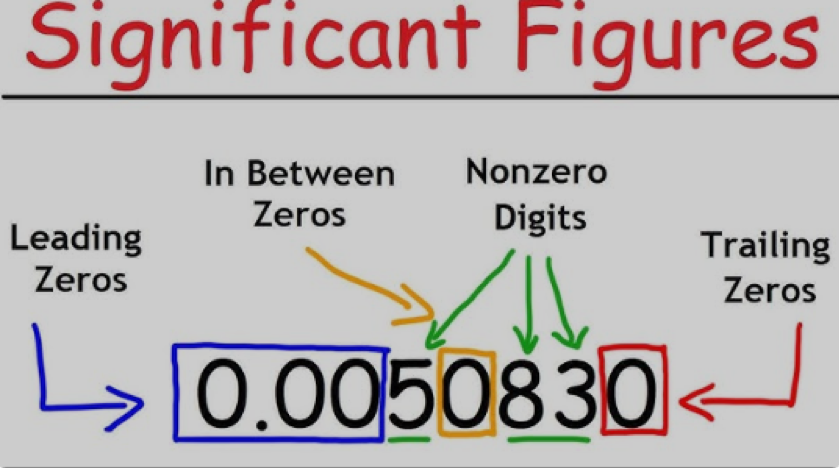
Guidelines for determining how many important figures are included in a measured quantity:
(1) Every digit that is not zero is important:
There are two significant digits for 1.2 g and four for 1.234 g.
(2) There is significance to zeroes in between nonzero digits:
3.07 mL has three significant digits, while 1002 kg has four.
(3) Zeroes that appear to the left of the first nonzero digit are only the decimal point’s location and have no significance:
There is just one significant
An “exact number”—what is it?
Certain numbers are precise because they can be known for sure.
The majority of exact numbers are integers: a foot is exactly 12 inches long, and a class may contain exactly 23 students. Precise figures are frequently seen as object counts or conversion factors.
One may argue that there are an endless amount of important figures for exact numbers. Consequently, the number of apparent significant numbers in any given actual number can be disregarded as a limiting factor when figuring out how many significant figures there are in the calculation’s outcome.
Guidelines for doing math operations
When performing computations, the basic rule is that the calculation’s least accurate measurement determines how exact the outcome can be.
The result of addition and subtraction is rounded to the final common digit that appears in every component that is farthest to the right. For instance, rounding to 124 (3 significant figures) from 100 (assuming 3 significant digits) + 23.643 (5 significant figures) yields 123.643.
When dividing and multiplying, the outcome must be rounded down to equal the component with the fewest significant figures in terms of the number of significant figures. To round off to 38, for instance, 3.0 (2 significant figures) − 12.60 (4 significant figures) equals 37.8000.
This rule states that the result is always rounded to the even digit if the digit to be decreased is 5, followed solely by zeroes. The idea behind this is to prevent bias in rounding: we round down 50% of the time and up 50% of the time.
general Recommendations for Calculator Use
When using a calculator, you might not be able to detect if an error has been made, or, even if you do, you might not be able to pinpoint the exact location of the fault if you complete a lengthy computation without recording any intermediate results.
Carry as many numbers as you can through the complete set of calculations in a lengthy calculation requiring mixed operations, and then round the result properly. For instance, 5.000 + 3.000 + 6.35 / 4.0 = 4.04858… + 3.000 + 1.5875 = 8.630829…
The three numbers added together should result in a number that is rounded off to the last common significant digit occurring furthest to the right (in this case, this means the final result should be rounded with 1 digit after the decimal). The first division should produce three significant figures, and the last division should produce two significant figures. 8.6 is the proper, rounded, result.
Conclusion
The number that is shown as digits is established using significant figures. These numbers are meaningfully represented by these digits. In place of figures, the phrase significant digits is also frequently used. Beginning with the first non-zero digit on the left, we can count all the values to determine the number of significant digits.